Data mining for marketing campaigns : interpretation of lift

This is a post about the lift of a data mining model for marketing campaigns.

(But if you want to keep it really simple, read first this really simple explanation of lift)

The topics discussed are :

• Definition
• Wait ! Why lift and not AUC ?
• Your selection size determines your lift
• Your target class proportion determines your lift
• How can you use lift for model comparison ?
• Large lifts, still small profits?
• To simplify : user returns in stead of lift

Definition (Wikipedia) : … measure of the performance of a model… The lift of a subset of the population is the ratio of the predicted response rate for that subset to the predicted response rate for the population.

Wait ! Why lift and not AUC ?
The Area Under the ROC-Curve is often cited as a better, geneal measure of the quality of the model. It allows you to compare different models. OK, right, but 1) try to explain AUC to your HiPPO’s. and 2) when you use your model for marketing campaigns you are only interested in the performance of a small selection of your customers, the ones with the best scores.
So : lift is simple, and you can make it even more simple. Read on.

Your selection size determines your lift
If you read the definition, you saw : … “lift of a subset of the population” … Normally you take a subset of the population with the best scores, the ones you would use in a campaign.
The size of your selection determines the upper limit of the lift.

• 100% of the population : lift is per definition = 1, meaning the performance of this selection = the performance of the total population. Of cause it is useless to make a data mining model and then use the entire population.
• 50% of the population : Upper limit = 2
• 25% of the population : Upper limit = 4
• 10% of the population : Upper limit = 10
• 5% of the population : Upper limit = 20
• 1% of the population : upper limit = 100
• etc.

You see it makes no sense to say : “my model has a lift of 10“. This means nothing. It depends for a great deal on the selection size.

 

• Your target class proportion determines your lift

 
Imagine you want to predict how many people in a selection will buy products A or B during,say, next week. Let’s say that normally you sell 100 pieces of A and 5,000 pieces of B in a week and the two products are equally predictable, meaning that the two data mining models are of comparable quality. So which model will show higher lifts for equal selection sizes ?
Again the proportion of the target class determines the upper limit of the lift :

• if you only have 5,000 customers in your database the lift for product B will be … 1. Since every client buys product B in a week you cannot get it higher with a model.
• if you have 50,000 customers, the highest possible lift will be 10. Why ? The proportion of buyers in the entire population is 10%. If with a very good model you can make a selection of 5000 (or less) where everyone buys than you get 100% buyers in your selection which is 10 times better => hence a lift of 10.
• if you have 5,000,000 customers and your model enables you to make a selection of 5,000 (or less) where everyone buys you compare 100% buyers with the 0.1% buyers in the entire population, which gives you a lift of 1,000 !

How can you use lift for model comparison ?

The way I do this is rather straightforward. I take the lift of all my models for the same selection size and plot the lift against the proportion of the target class.

This gives something like this with lift on the vertical axis and selection size on the horizontal axis :

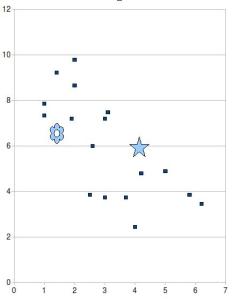
See that the star is lower than the flower ? Nevertheless the “star” model is of better quality because its lift is one of the best compared with the other models, whereas the “flower” model is relatively poor.

Large lifts, small profits ?
What does a large lift mean for the return of a marketing campaign ? Absolutely nothing !
The return of a marketing campaign depends on (among others) :

• the fixed costs for the campaign (making the model, paying for the administration,
• the variable costs for the campaign (paying for the publicity, costs per letter when using snail mail, ….)
• The number of surplus sales (= the number of sales in the campaign minus the “normal” number of sales : expected number if you did no campaign)
• the gain in $ per surplus sale

So where does the data mining model come in ? The number of surplus sales depends on the impact of the e-mail, letter, phone call on the client behaviour : will he/she buy, whereas without the e-mail he/she would not ? If thanks to the data mining model you selected a very good target group the impact will be bigger.
And now the lift :
Case A : 1) normally you sell a 1,000 pieces to 5% of your customers. 2) You select a target group of 5,000 customers with a sales rate of 10% (=> lift = 2). 3) the e-mail impact doubles the success rate which means that you sell 1,000 pieces to that target group of 5,000 customers. Hence you get 500 surplus sales.
Case B : 1) normally you sell a 20 pieces to 0,1% of your customers. 2) You select a target group of 100 customers with a sales rate of 1% (=> lift = 10). 3) the e-mail impact doubles the success rate which means that you sell 20 pieces to that target group of 100 customers. Hence you get 10 surplus sales. If each sale of product A is worth the same amount of $ as product B it is clear that the high lift in case B is worth much less than the lower lift of product A.
Lift is just … lift. You have to lift something. It means more to life a huge quantity a little bit than a tiny quantity a lot.

So do not waste your time to develop targeting models for products that do not sell !

To simplify : user returns in stead of lift
For some HiPPO’s lift is still something too complicated. In that case use a simple return chart : take the lift chart in this post, but replace the life by the percentage of buyers. It is very easy and it is much more business language. You can directly tell if using the model is worth wile.

%-age of positive targets in relation to the selection size

Notice that the “lift curve” shows how much the %-age of positive targets is “lifted” above the baseline (random selection).

Other posts you might enjoy reading :
Howmany inputs do data miners need ?
Oversampling or undersampling ?
data mining with decision trees : what they never tell you
The top-10 data mining mistakes
Good enough / data quality